| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 프로세스
- 데드락
- BFS
- 알고리즘
- Memory Management
- 운영체제
- BOJ
- paging
- Deadlock
- samsung research
- 컴공복전
- 스케줄링
- 구현
- 김건우
- fork
- exec
- 삼성기출
- 삼성리서치
- ascii_easy
- segmentation
- 동기화문제
- higunnew
- Brute Force
- dfs
- 가상메모리
- pwnable.kr
- 백준
- 완전탐색
- 시뮬레이션
- 백트래킹
- Today
- Total
gunnew의 잡설
2. Linear Regression Using Tensor Flow 본문
(1) 선형 회귀란?
선형 회귀라... 나는 경제학과이다. 경제학을 열심히 공부하던 때, 나는 선형 회귀라는 말을 참 많이 들었다. 계량 경제학을 공부하면 많이 나오는 말이란다. 그런데 나는 이 단어가 참으로 현학적으로 느껴졌다. 어떤 수업에서 이 주제로 발표하던 학생이 "OLS 다들 아시죠?" 하는 질문에 냉소를 지었던 기억이 나기도 한다. 도대체 선형 회귀 (Linear Regression)은 무엇일까? 저 regress라는 말을 사전에 찾아보면 돌아가다. 회귀하다. 라는 뜻이 나온다. 그게 도대체 분석과 무슨 관련이 있단 말인가. Linear Regression이라는 단어를 처음 듣는 사람이 이해를 못하게 되는 것은 당연하다.
일기장이 되어가는 것 같아 여기서 그만하고, 선형 회귀에 대해 설명해보자. 아주 아주 상식적인 선에서 우리가 어떤 현상에 대해 '이럴 것이다~' 하고 추측해보는 상황에 있다고 생각하자.
일단 내가 리그 오브 레전드라는 게임을 한다고 가정하자(사실 가정이 아니다). 그리고 정말 정말 상식적으로 생각했을 때, 게임에 투자한 시간이 많다면 롤 티어가 더 높을 것이라 생각할 수 있겠다(세상이 꼭 그렇지는 않았다). 아무튼, 내 친구 민다는 롤을 지금까지 1200시간 플레이하였다. 티어는 실버이다. 또 다른 친구 복재는 롤을 지금까지 1500시간 가량 플레이하고도 티어는 골드이다(사람이 그럴 수 있나?). 나는 대략 2000시간 가량 플레이하였고 티어는 플래티넘이다. 롤은 총 9개의 티어가 있기 때문에 편의상 오름차순으로 낮은 티어부터 높은 티어까지 각각 1에서부터 9까지의 값을 배정하겠다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 아이언 | 브론즈 | 실버 | 골드 | 플래티넘 | 다이아몬드 | 마스터 | 그랜드마스터 | 챌린저 |
그리고 내가 가진 정보를 표로 나타내면 다음과 같다.
| 플레이 시간 | 티어 |
| 1200 | 3 |
| 1500 | 4 |
| 2000 | 5 |
자, 대충 비례 관계가 보일 것이다. 정확하진 않지만, 플레이 시간 * 1/400을 하면 티어가 나오는 것을 확인할 수 있다. 따라서 우리의 가설을 T(티어) = 1/400 * X(플레이 시간) 이라고 생각할 수 있겠다.
이것이 아주 직관적인 선형 회귀이다. 어떤 변수 간의 관계를 일차 함수의 형태(선형 함수)로 나타내고 그 나머지를 오차로 설정하여 모델로 설정해 놓는 것이 선형 회귀(Linear regression)이다.
그런데 이것은 사람이 눈으로 할 수 있는 계산량이기 때문에 쉽게 모델을 한눈에 예측할 수 있었다. 그러나 정말 복잡하고 많은 데이터가 주어진다면 이렇게 쉽게 예측하기 어려울 것이다. 또한, 컴퓨터는 초깃값을 스스로 적당한 값을 설정하지 못한다. 바로 이 지점이 머신러닝의 힘이 발휘되어야 하는 지점이다. 과연, 데이터만 주어진 상태에서 우리가 세우고자 하는 가설 혹은 모델에, 컴퓨터는 어떻게 정확하게 근사할 수 있을까?
(2) Minimizing Sum of Squared Error
"아니, 지금 아는 척하려고 영어 쓰시는 거예요?" 가 아니라 딱히 저 말을 한국어로 번역하고 싶지가 않았다. 한국어로 번역한다 해도 이해가 안되기는 마찬가지이다(에러 제곱의 합을 최소화?). 왜 굳이 에러의 제곱을 최소화하는 것일까? 그냥 에러의 합을 최소화하는 것은 안될까? 안된다. 왜? 그 이유는 선형 함수에서 기울기를 완전히 잘못 설정하더라도, 평균 지점만 지나가게 되면 Error의 합은 작아질 것이기 때문이다. 그래서 항상 Error에 해당하는 값이 항상 양수가 되도록 이들의 제곱을 사용하는 것이다. 이것을 Cost 함수라고 칭한다.
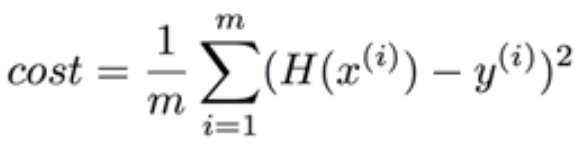
와 같이 쓸 수 있겠다. m으로 나눠줘도 되고 안 나눠줘도 된다. 인터넷에서 가져온 수식이 나눠준 식이기 때문에 나눠준 것으로 생각하자. H(x)는 우리가 세운 가상의 관계식이다. wx + b.
그리고 y는 실제 데이터들을 의미한다. 이들의 차를 제곱한 것을 다 더해준 것이 시그마의 식이다. 우리는 저 함수를 최소화하는 H(x) = wx + b에서 w와 b를 구할 것이다(여기서 w는 weight, 가중치, b는 bias, 편의를 의미함).
(3) 텐서플로우로 구현
"뭐했다고 벌써 구현해요?" 근데 딱히 달리 설명할 방법이 없다. 이보다 더 쉽게 설명하기 위해서는 고등학교 수학부터 언급해야 한다. 아무튼 그럼 텐서플로우로 어떻게 구현할까? 구현하기에 앞서 대충 생각해보자.
"일단 노드에 operation을 넣어야 하는데... 우선 w랑 b 노드에 아무 값이나 하나 넣어야겠지? 근데 이건 계속 바뀌어야 하니까 저번 시간에 배웠던 constant를 쓰면 안될 것 같은데?.. 구글링 해보자. Variable이라는 operation이 있나보다!"
텐서플로우에서 Variable을 사용하는 방법은
tf.Variable(<init value>, name = ' ')이다.
자 그렇다면 학습시킬 데이터를 컴퓨터한테 던져 주고, 초깃값을 설정해주자. 초깃값 설정 방법에는 여러 가지가 있지만 여기서는 아무 값이나 1개 할당해 주는 방법을 사용하였다. 위의 롤 예시는 너무 구리니 그냥 일반적인 예시로 하겠다.
X = [1, 2, 3]
Y = [2, 3, 4]
# trainable 한 variable이다. 텐서플로우가 학습하는 과정에서 변경시킨다.
# shape이 어떻게 되는가? 값이 하나인 일차원 array, rank가 1인
W = tf.Variable(tf.random_normal([1]), name = "weight")
b = tf.Variable(tf.random_normal([1]), name = "bias")대충 보면 Y = 1 * X + 1이 나와야 한다고 생각할 것이다. 이제 귀찮으니 그만하자.
그리고 우리가 세운 가설 노드도 설정해 줘야 한다.
hypothesis = W * X + b자, 그리고 윗장에서 배운 Minimizing Sum of Squared Error를 사용하여 cost function 노드를 만들어보자.
cost = tf.reduce_mean(tf.square(hypothesis - Y))tf.square(hypothesis - Y)를 통해 Squared Error를 구했고, tf.reduce_mean( )을 통해 Squared Error의 평균을 최소화하게 될 것이다.
이제 대망의 '그 부분'이다. 아 물론, '그 부분'에 대해 설명한 적은 없지만 정말 중요한 부분이라는 의미이다. 다음 코드를 잘 이해해보자.
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())optimizer라는 노드에 텐서플로우의 GradientDescentOptimizer를 learning_rate = 0.01로 할당하였다. 도대체 이건 무슨 뜻인가? GradientDescentOptimizer는 뜻만 놓고 보면 경사 하강 최적화이다. 좀 더 나아가보면, 초깃값으로 부터 시작하여 해당 위치에서 cost function에 대한 미분계수를 이용하여 조금씩 조정해 보겠다는 소리이다. 그림으로 간략히 이해해보면 다음과 같이 진행된다.
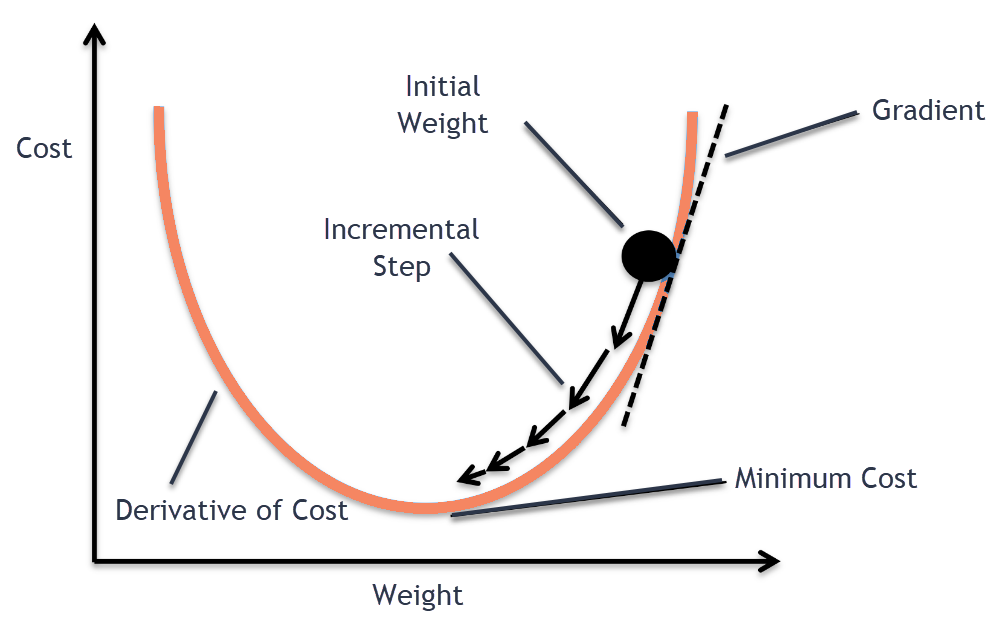
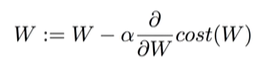
"오우야.." 수학을 잘 모르는 사람이 본다면 탄식이 나올 수 밖에 없다. 하지만 어쩔 수 없다. 머신러닝은 수학적 베이스가 탄탄해야 한다고 한다. 미분과 편미분에 대한 기본적인 지식이 있다고 생각한다면 위 식은 아무 것도 아니다. 저기서 alpha가 바로 우리가 지정했던 learning_rate이 된다. 따라서 learning_rate을 너무 크게, 혹은 너무 작게 설정하면 머신러닝의 효율이 떨어지기에 적절히 잘 설정해야 한다.
다시 돌아와서 밑의 코드를 살펴보자.
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())위 optimizer를 가지고 cost를 minimize 할 것이고 이 operation을 다시 train에 넣어 준다. 세션을 만들고, 이제 실제로 텐서플로우 머신러닝을 위해 global_variables들을 초기화해야 하는데 이는 tf.global_variables_initializer()함수를 이용한다. 우리가 앞에서 W와 b를 Variable로 설정하였다. 이 안에는 어떤 값이 들어와야 한다는 정보만 주었지 정말 초기화 된 상태가 아니다. 따라서 Variable로 노드를 설정했으면 꼭 초기화를 해주자.
이제 for문을 돌며 러닝을 해줄 차례이다. 다음은 전체 코드이다.
X = [1, 2, 3]
Y = [2, 3, 4]
# trainable 한 variable이다. 텐서플로우가 학습하는 과정에서 변경시킨다.
# shape이 어떻게 되는가? 값이 하나인 일차원 array, rank가 1인
W = tf.Variable(tf.random_normal([1]), name = "weight")
b = tf.Variable(tf.random_normal([1]), name = "bias")
hypothesis = X * W + b
cost = tf.reduce_mean(tf.square(hypothesis - Y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.1)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(train)
if step % 20 == 0:
print(step, sess.run(cost), sess.run(W), sess.run(b))2001번의 loop를 돌며 20의 배수마다 training된 데이터를 출력하게 하였다. 그리고 train 이라는 노드에 들어간 operation graph를 계속해서 학습할 것이다. 와우! 근데 어떻게 그 복잡한 개념들이 sess.run(train) 단 한 줄에 들어갈 수 있는 것이지? 텐서플로우는 이러한 강력한 데이터 플로우를 쉽게 구현할 수 있게 만들어 준다.
train -> optimizer.minimize(cost) -> cost = reduce_mean(sqaure(hypo - Y), optimizer -> GradientDescentOptimizer -와 같은 흐름들을 train의 실행만으로도 모든 연산을 자동으로 해주는 것이다.
| 만약 GradientDescentOptimizer가 없다면? 우리가 직접 미분하여 식을 계산한 후 다음과 같은 코드를 쳐주어야 한다. 게다가 cost function이 위처럼 polynomial 형태가 아니라 미분 불가능하거나 미분하기 너무 힘든 경우에는 어떠한가? |
cost = tf.reduce_sum (tf.square(hypothesis - Y))
learning_rate = 0.01
# (W*X - Y)^2를 미분
gradient = tf.reduce_mean((W * X - Y) * X)
# W = W - learning_rate * 미분계수
descent = W - learning_rate * gradient
# W를 descent로 업데이트 할 때 assign 메소드를 사용해야 함.
update = W.assign(descent)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(21):
# update를 세션으로 실행해야 함.
sess.run(update, feed_dict = {X : x_data, Y : y_data})
print(step, sess.run(cost, feed_dict = {X : x_data, Y : y_data}), sess.run(W))출력 결과를 일부만 살펴보자.
1800 3.0790184e-13 [1.0000007] [0.99999845]
1820 3.0790184e-13 [1.0000007] [0.99999845]
1840 3.0790184e-13 [1.0000007] [0.99999845]
1860 3.0790184e-13 [1.0000007] [0.99999845]
1880 3.0790184e-13 [1.0000007] [0.99999845]
1900 3.0790184e-13 [1.0000007] [0.99999845]
1920 3.0790184e-13 [1.0000007] [0.99999845]
1940 3.0790184e-13 [1.0000007] [0.99999845]
1960 3.0790184e-13 [1.0000007] [0.99999845]
1980 3.0790184e-13 [1.0000007] [0.99999845]
2000 3.0790184e-13 [1.0000007] [0.99999845]첫 번째 값은 loop_counter이고, 두 번째가 cost, 즉, 오차의 제곱의 평균이다. 거의 0에 수렴한다. 그리고 세 번째와 네 번째가 각각 W와 b이다. 1과 1에 수렴하는 것을 알 수 있다.
(4) 세 줄 요약
- Minimizing Sum(or Mean) of Square Error의 개념을 이해하자.
- GradientDescentOptimizer을 기억하고 learning_rate 잘 설정하자.
- global_variable_initializer()를 잘 쓰자.
끝.
'TensorFlow' 카테고리의 다른 글
| 3. Multi-variable linear regression (0) | 2019.11.10 |
|---|---|
| 1. Why Tensor Flow? (2) | 2019.11.10 |


