| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- pwnable.kr
- 동기화문제
- paging
- BFS
- segmentation
- 알고리즘
- 삼성리서치
- samsung research
- Deadlock
- 백준
- BOJ
- 시뮬레이션
- 김건우
- 구현
- Brute Force
- 가상메모리
- higunnew
- 데드락
- dfs
- 컴공복전
- ascii_easy
- 삼성기출
- 운영체제
- Memory Management
- exec
- 백트래킹
- fork
- 프로세스
- 완전탐색
- 스케줄링
- Today
- Total
gunnew의 잡설
BOJ_15684_사다리조작(C++) [DFS Back tracking] 본문
PS 백준 소스 코드 모음 : https://github.com/kgw4073/Problem-Solving
https://www.acmicpc.net/problem/15684
15684번: 사다리 조작
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다. 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다. 초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다. 가로선은 인접한 두 세로선을 연결해야 한다. 단, 두 가로선이 연속하거나 서로
www.acmicpc.net
이 포스팅은 적어도 내가 백준 온라인 저지에 있는 이 문제집을 다 풀기 전까지는 계속 업로드할 것이다.
https://www.acmicpc.net/workbook/view/1152
문제집: 삼성 SW 역량 테스트 기출 문제 (baekjoon)
www.acmicpc.net
처음 이 문제를 풀기 시작했을 때는 조금 막막했다. 완전 탐색인 것 같기는 한데 조금 더 나은 방식으로 최적화를 할 수 있을 것이라 생각했기 때문에 약 한 시간 반을 아무것도 하지 않고 오로지 생각만 하다가 날렸다. 어느 정도 그 실마리를 찾긴 했지만 이것을 코드로 구현하자니 답이 나오지 않았다. 내 부족한 머리로는 완전 탐색 이외의 더 나은 최적화 방안을 코드로 밖에 구현할 수 없다는 것을 깨달았다. 만약 이런 정지 상태가 실제 코테 시험장에서 일어난다는 생각을 하니 너무 암울했으나 아무튼 3시간 안에 풀어야 했으니 꽤나 압박감에 시달리며 코드를 쓰기 시작했다.
결론부터 말하면 약 3시간 30분에 걸쳐 완성하였다. 정답률이 20%로 꽤나 낮은 편에 속했기 때문에 기분이 좋았지만 시험장이었다면 제 시간 안에 풀지 못하고 나왔을 것이라는 생각을 하니 한 편으로는 마음이 답답했다.
내 일기는 여기서 마치고 이제 풀이로 들어가보자.
다음 그림을 가만히 보고 있다 보니 일단 세로 선들 1번부터 5번까지 차례대로 탐색해야 할 것이라는 생각이 들었다. 내가 현재 1번 세로 선을 탐색한다고 가정하자. 그럼 먼저 자동으로 (1, 1) -> (1, 2)인 가로 선을 거쳐 (2, 2)에 도달할 것이다. 이 지점에는 가로 선이 없으므로 나의 선택은 총 세 가지가 있다.
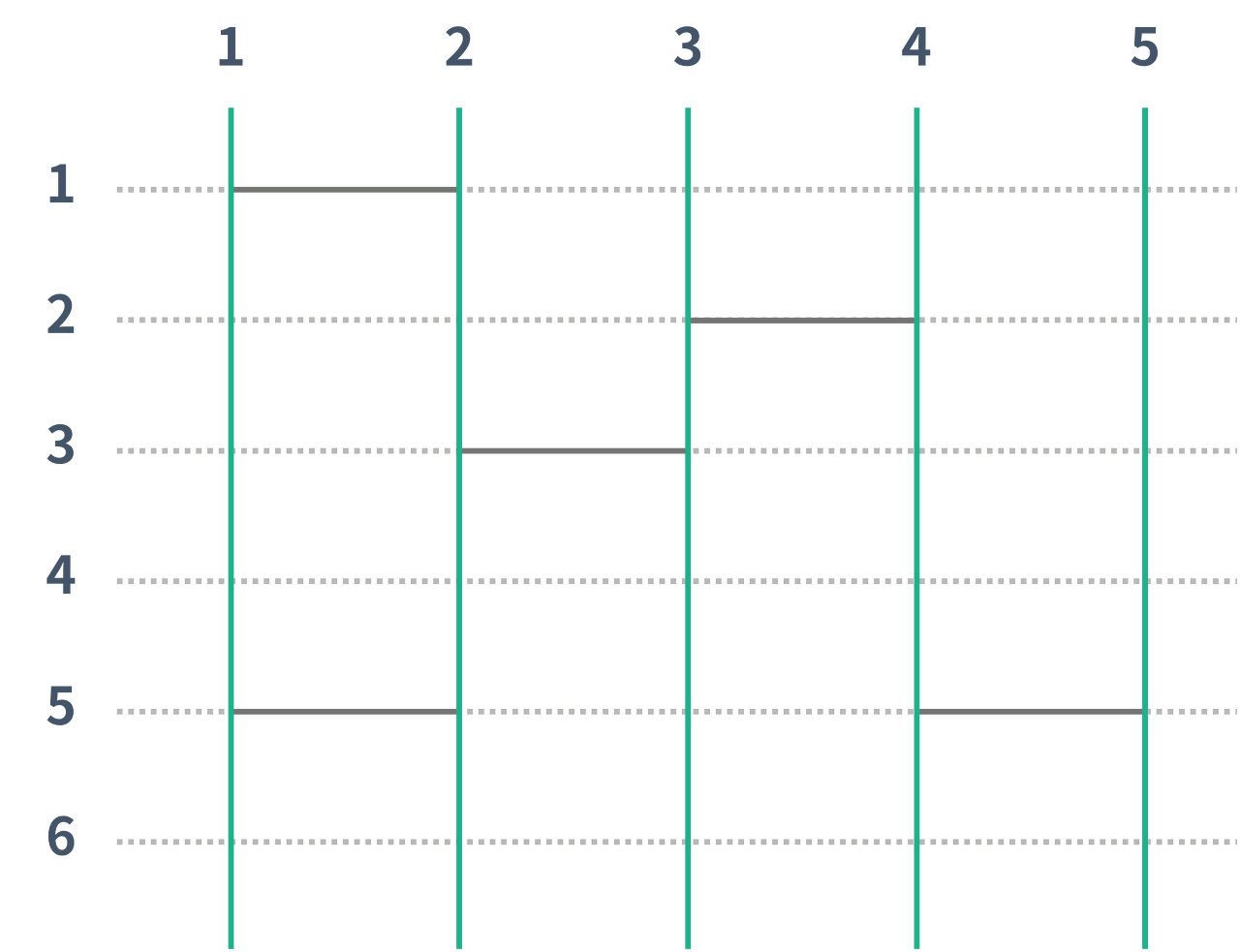
1. 오른쪽으로 가로 선을 놓는다.
2. 왼쪽으로 가로 선을 놓는다.
3. 그냥 밑으로 내려간다.
다만 가로 선을 추가할 수 있는 조건이 문제에 존재하므로 조금 더 정확히 정리하여 일반화된, 일종의 조건 점화식을 작성한다면 다음과 같을 것이다.
|
해당 점에 오른쪽 가로 선이 있다면 : 오른쪽 가로 선 타고 무조건 내려감 해당 점에 왼쪽 가로 선이 있다면 : 왼쪽 가로 선 타고 무조건 내려감
해당 점에 가로 선이 오른쪽 왼쪽 둘 다 없다면 { 두 칸 오른쪽에 가로 선이 없는 경우 { 오른쪽 가로 선을 놓고 타고 내려가 봄 } 두 칸 왼쪽에 가로 선이 없는 경우 { 왼쪽 가로 선을 놓고 타고 내려가 봄 } 사다리 놓지 않고 그냥 밑으로 내려가 봄 } |
그런데 왜 무조건 내려감과 내려가 봄을 구분했는가? 무조건 내려간다는 것은 사다리를 놓을 필요가 없이 있으면 항상 타고 내려가야 한다. 그러니까 무조건 내려가는 경우에는 그냥 말 그대로 내려가면 끝이다. 그러나 '내려가 본다'는 의미를 잘 생각해보자. 일단 사다리 놓고 내려간 다음에, 그 길이 틀렸다면 다시 돌아와서 사다리를 철거해야 한다는 의미이다. 이것이 DFS의 핵심이다.
이 조건 점화식을 (조건 점화식이라 하는 것은 백트래킹과 DFS를 설명할 때 내가 설명하기 편하게 하기 위해 만든 단어다. 실제로는 아마 없을 것) 코드로 살펴보면 '아하!' 하고 재귀 함수를 통한 완전 탐색이 직관적으로 이해될 것이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
void solve(int start, int y, int x, int add, int rmap[][11], int map[][11]) {
// 모든 세로 선을 다 탐색하고 도달했다면 answer를 갱신
if (start == n + 1) {
answer = min(answer, add);
return;
}
// 범위를 벗어났거나 원래 시작했던 세로 선에 도달하지 못했다면 실패
if (x <= 0 || x > n || (y >= h + 1 && x != start)) return;
// 가로 끝에 내려왔는데 시작한 세로 선이라면 다음 세로 선을 탐색
if (y >= h + 1 && x == start) {
solve(start + 1, 1, start + 1, add, rmap, map);
return;
}
// 오른쪽 가로 선 있다면 타고 내려감
if (map[y][x]) {
solve(start, y + 1, x + 1, add, rmap, map);
}
// 왼쪽 가로 선 있다면 타고 내려감
if (rmap[y][x]) {
solve(start, y + 1, x - 1, add, rmap, map);
}
// 둘 다 없으면
if (!map[y][x] && !rmap[y][x]) {
// 현재 추가된 사다리가 2이하일 때만 하나 더 놓을 수 있음
if (add <= 2) {
if (!map[y][x + 1]) {
map[y][x] = 1;
rmap[y][x + 1] = 1;
solve(start, y + 1, x + 1, add + 1, rmap, map);
rmap[y][x + 1] = 0;
map[y][x] = 0;
}
if (!rmap[y][x - 1]) {
map[y][x - 1] = 1;
rmap[y][x] = 1;
solve(start, y + 1, x - 1, add + 1, rmap, map);
map[y][x - 1] = 0;
rmap[y][x] = 0;
}
}
// 그냥 내려가 봄
solve(start, y + 1, x, add, rmap, map);
}
}
|
cs |
위에서 설명한 조건 점화식을 그대로 코드로 옮겨 놓은 것뿐이라는 것을 확인할 수 있다. 다만, 인자로 map과 rmap을 두었는데 map은 오른쪽으로 가는 사다리를, rmap은 왼쪽으로 가는 사다리를 나타낸다. map 하나로만 해도 되지만 직관적으로 왼쪽으로 가는 것과 오른쪽으로 가는 것을 구분하기 위해 따로 배열을 두었다.
풀 코드 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
#include <iostream>
#include <algorithm>
using namespace std;
int n, m, h;
int map[32][11];
int rmap[32][11];
const int inf = 2e9;
int answer = inf;
void solve(int start, int y, int x, int add, int rmap[][11], int map[][11]) {
// 모든 세로 선을 다 탐색하고 도달했다면 answer를 갱신
if (start == n + 1) {
answer = min(answer, add);
return;
}
// 범위를 벗어났거나 원래 시작했던 세로 선에 도달하지 못했다면 실패
if (x <= 0 || x > n || (y >= h + 1 && x != start)) return;
// 가로 끝에 내려왔는데 시작한 세로 선이라면 다음 세로 선을 탐색
if (y >= h + 1 && x == start) {
solve(start + 1, 1, start + 1, add, rmap, map);
return;
}
// 오른쪽 가로 선 있다면 타고 내려감
if (map[y][x]) {
solve(start, y + 1, x + 1, add, rmap, map);
}
// 왼쪽 가로 선 있다면 타고 내려감
if (rmap[y][x]) {
solve(start, y + 1, x - 1, add, rmap, map);
}
// 둘 다 없으면
if (!map[y][x] && !rmap[y][x]) {
// 현재 추가된 사다리가 2이하일 때만 하나 더 놓을 수 있음
if (add <= 2) {
if (!map[y][x + 1]) {
map[y][x] = 1;
rmap[y][x + 1] = 1;
solve(start, y + 1, x + 1, add + 1, rmap, map);
rmap[y][x + 1] = 0;
map[y][x] = 0;
}
if (!rmap[y][x - 1]) {
map[y][x - 1] = 1;
rmap[y][x] = 1;
solve(start, y + 1, x - 1, add + 1, rmap, map);
map[y][x - 1] = 0;
rmap[y][x] = 0;
}
}
// 그냥 내려가 봄
solve(start, y + 1, x, add, rmap, map);
}
}
int main() {
cin >> n >> m >> h;
// 오른쪽으로 가는 선과 왼쪽으로 가는 선을 map과 rmap으로 저장
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
map[u][v] = 1;
rmap[u][v + 1] = 1;
}
solve(1, 1, 1, 0, rmap, map);
if (answer == inf) {
cout << -1;
}
else {
cout << answer;
}
}
|
cs |
'Algorithm' 카테고리의 다른 글
| BOJ_17825_주사위윷놀이 [DFS by Back Tracking] (0) | 2020.01.30 |
|---|---|
| BOJ_5373_큐빙 [Brute Brute Brute Forcing, Simulation] (0) | 2020.01.26 |
| BOJ_12100_2048(C++) [Brute forcing by DFS] (0) | 2020.01.21 |
| BOJ_13460_구슬탈출(C++) [BFS] (0) | 2020.01.19 |
| BOJ_14501_퇴사(C++) [DFS or Dynamic Programming] (1) | 2020.01.11 |




